My recent research evolved in several directions, for example rapidly rotating gases and fractional quantum hall physics,
novel consequences of strong interactions in lattices,
and reduced dimensional quantum gases.
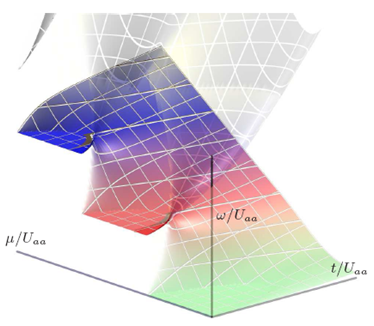
The rf spectrum as a function of chemical potential and hopping rate with
opacity indicating spectral weight; 20% different initial and final state interactions.
Another fascinating direction has emerged: by studying spectroscopy of ultracold atomic gases, we
learn what these probes reveal about many-body systems.
Our analysis of
experiments in Ketterle's group at MIT has revealed that these spectra directly
elucidate the various
correlations of superfluid lattice bosons near their instability to the Mott insulating state.
The general understanding of this basic but
non-trivial system is relevant to other quantum phase transitions.
More details: our "big picture" goals require improved probes
Cold atoms offer
many appealing features for studying many-body systems: (i) one knows exactly the
Hamiltonian,
which often is a canonical solid state model, such as a Hubbard model; (ii) they are quantum coherent
on experimentally relevant timescales --- they couple to no bath; and
(iii) their behavior is readily tunable: for example, one may greatly vary the
interaction strength, band structure, and internal spin structure.
However, our probes at the moment are rather blunt. The most common is absorption imaging, which
provides real space column-integrated densities.
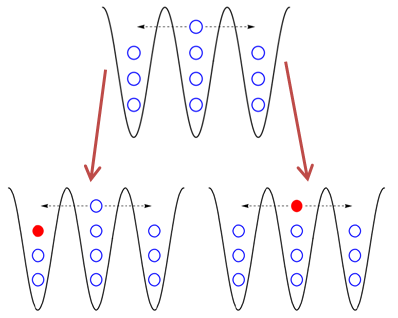
Top: cartoon of superfluid near the Mott instability,
for average site fillings slightly greater than 3. Near the Mott state,
the superfluid state looks like a Mott insulator with a few delocalized particles or holes dispersed on it. Bottom:
After absorbing an rf photon to change an atom's internal state, there are two possible final states, each with
different energies, leading to a bimodal rf spectra.
Roughly, each point in the trap corresponds to a different local chemical
potential and consequently the density profile gives the equation of state. Although useful,
this fails to
directly probe much interesting physics,
e.g. the elementary excitations
and collective modes of the system. One may demonstrate how little information
density profiles contain by comparing them
distinct systems. One finds that non-interacting fermions, strongly
interacting fermions, Bose-Einstein condensates all have qualitatively similar density profiles. Near the center (at high
densities) the density depends on the trap position via a power law, and in the
tail the dilute thermal gas yields a Gaussian shape. Indeed, virtually any
physical system displays this generic behavior.
In contrast, spectroscopies cleanly distinguish these scenarios by probing their excitations:
each has a characteristic number of excitations, gapless or gapped
dispersion, and spectral weight distribution.
Erich and I have concentrated on rf-microwave spectroscopy of bosons in an
optical lattice, in which absorbed photons change only the internal state of
atoms. Hazzard and Mueller, PRA
76 063612 (2007) calculated the
trap-averaged rf spectra, using a sum rule approach assuming that
the local spectrum was a single delta function. As a follow up, we have been
investigating the full local structure of the rf spectra.
In work being prepared for publication, we find that the superfluid near the
Mott instability displays a multi-peaked spectrum, one peak with "Mott"
and one with "delocalized" behavior; the dual nature of these correlations
are illustrated to the left. The
characteristic spectral densities are to the right and at the top right of the
page.
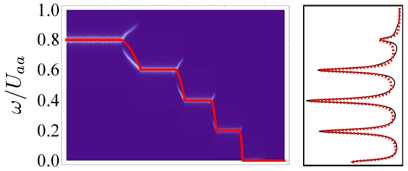
Left: spectral
density as a function of frequency and distance to trap center (white).
Right: trap averaged spectral density (solid) versus frequency (on vertical
axis). Red curves are predictions of the sum rule approach.
I believe rf spectroscopy will continue to play an important role in cold atoms. For vanishing final state
interactions, rf spectra are quasi-hole spectra; for equal final and initial state interactions,
it is an analog of Bragg
scattering/spectroscopy and transport measurements. Each are standard,
powerful solid state probes. By
varying the final state interaction, we may mimic these techniques and additionally
"interpolate" between these two limits. Consequently, although the
present theory and experiment has largely restricted to zero momentum
excitations, extending this work to finite momenta would be valuable. I hope that our work enables an even better understanding
of the bosonic Mott
insulator and helps pave the way for further application of spectroscopy to cold
atomic many body systems.