Ultracold atoms, molecules, ions, and photons are incredibly clean, tunable, and
unique many-body systems. Experimental tools enabled by decades of
progress understanding and engineering light-matter interactions allow
experimentalists to tunably realize a huge variety of Hamiltonians and quantum
states.
One thread of my research revolves around the fact that one can engineer
many-body systems described by canonical models of condensed matter physics.
I find ways to use cold atom "quantum simulations" of these models to solve open,
important problems in other fields of physics, such as condensed matter. This includes schemes to
extract information about these systems, to engineer broader varieties of models, and
to reach important phases of matter or nonequilibrium behaviors. I'm
especially interested in behavior that is beyond the remarkably successsful Fermi
liquid/broken symmetry lines of thought. Prominent examples are quantum critical
points and exotic phases such as topologically ordered states and gapless spin
liquids. I am also interested in more than mimicking known phenomena, but in exploring the new phenomena that ultracold matter can display unavailable elsewhere in nature.
Another thread revolves around using the advanced capabilities of atomic and
molecular optics to generate quantum states that enable capabilities unavailable
to classical systems. One example is squeezed states, which are useful for
metrology or sensing beyond the standard quantum limit. Another example
involves quantum communication and computation. I am particularly
interested in finding other classes of resources that may be created without
requiring the full technology of a quantum computer implemented in each physical
system.
Below, I describe a few problems the group has studied. It's hopelessly out of date, but it still gives an impression of our interests.
Polar molecules
Ultracold polar molecules are a recent addition to the ultracold family. Far more than just "another degenerate system,"
polar molecules may offer transformative capabilities to emulate many-body quantum magnetism.
They also promise
applications in quantum information and precision measurement of fundamental
quantities.
Two properties underly these possibilities. First, molecules possess many
long-lived internal states (rotational, vibrational, hyperfine, and electronic),
which can mimic spin degrees of freedom. Second, dipolar interactions give
strong spin-spin interactions, orders of magnitude larger than their
superexchange-driven analogs in atomic systems. Furthermore, we have shown
that by applying
microwaves and dc electric fields
one can realize an incredible range of models:
e.g. XYZ or SU(N) Heisenberg models, compass-like models possessing
"symmetry protected topological" phases, and -- at least if one possesses enough
faith in the eventual experimental capabilities! --
the Kitaev model.
More immediately, we have shown how ongoing experiments -- even if
non-degenerate and in sparsely occupied lattices -- can
use
far-from-equilibrium dynamics induced by experimentally routine Ramsey
spectroscopy to benchmark quantum emulation of models, create useful entangled
states, and explore novel regimes of dynamical behavior. The
JILA Research
Highlight "Model Behavior" gives a broad overview of this work.
We have also studied Rabi spectra as a diagnostic tool.
We have continuing collaboration with
Jun Ye and
Debbie Jin on thhse and other
topics.
Trapped ions
Trapped ions are a relatively mature platform for quantum science. They
enable for example,
incredibly precise atomic clocks (losing only one second in billions of
years) and quantum information processing, for example
realizing two-qubit gates
with greater than 99% fidelity. Because ions are charged, they interact via
strong Coulomb interactions, leading to favorable energy scales for cooling and length scales for
imaging and manipulation.
Recently, these tools have been applied to quantum
emulation, especially of spin models. Electron spin, electronic, or
hyperfine levels can function as spins while interactions are mediated through
vibrations of the Coulomb crystal.
Chris Monroe and
Rainer Blatt's groups
are at the forefront of these experiments on typically 5-15 ions.
A particularly exciting development has been Penning trap experiments by John
Bollinger's group at NIST-Boulder applying this to crystlas of 100-300 ions.
At this number of particles, the properties are far beyond what theory can
generally treat exactly, and we expect to learn much.
Motivated by this surge of experiments we are developing theoretical techniques
for these systems' many-body behavior. One advance has been
the first solution of an interacting many-body problem with
local decoherence, which remarkably is for the same model describing the simplest
ion trap experiments. We are now extending this to even more
exciting regimes and devising better ways to produce useful quantum states.
Alkaline earth atoms
Experimentalists can now cool alkaline earth-like atoms (e.g., Sr, Ca, Yb) to
quantum degeneracy. Due to their special electronic structure, these have
unique applications to
quantum
emulation,
atomic clocks
and
quantum information.
For example, they can realize SU(N) symmetric spin
interactions for N as large as 10. The Hilbert space for N=10 is the same as a spin-9/2, but rather than becoming
classical for large N the SU(N) symmetry keeps quantum fluctuations important. As
one dramatic example, in the large-N limit,
these can
realize topologically ordered chiral spin liquids.
I have explored the presently experimentally
relevant "high temperature" regime where temperature > tunneling. Remarkably, we found that if one
adiabatically loads a lattice fixing initial gas conditions in an
experimentally relevant way and increases N, the states obtained become
substantially colder, even relative to interesting scales (e.g. the Mott gap). To explore
the behavior and especially to what extent this effect persists to lower
temperature, we considered one-dimensional systems where specialized techniques apply
(e.g., Bethe ansatz, bosonization, DMRG, and sign-problem-free QMC).
Remarkably, in one dimension we found that the decrease in temperature with
increasing N not only continued to apply to low temperatures
(temperature << tunneling), but
became more dramatic!
In conjunction, we
thoroughly studied the correlations, entanglement, and quantum state
properties of the T=0 phases and phase transitions.
See the
JILA Research Highlight "New Flavors of Quantum Magnetism" for another broad
perspective on this work.
Far from equilibrium dynamics
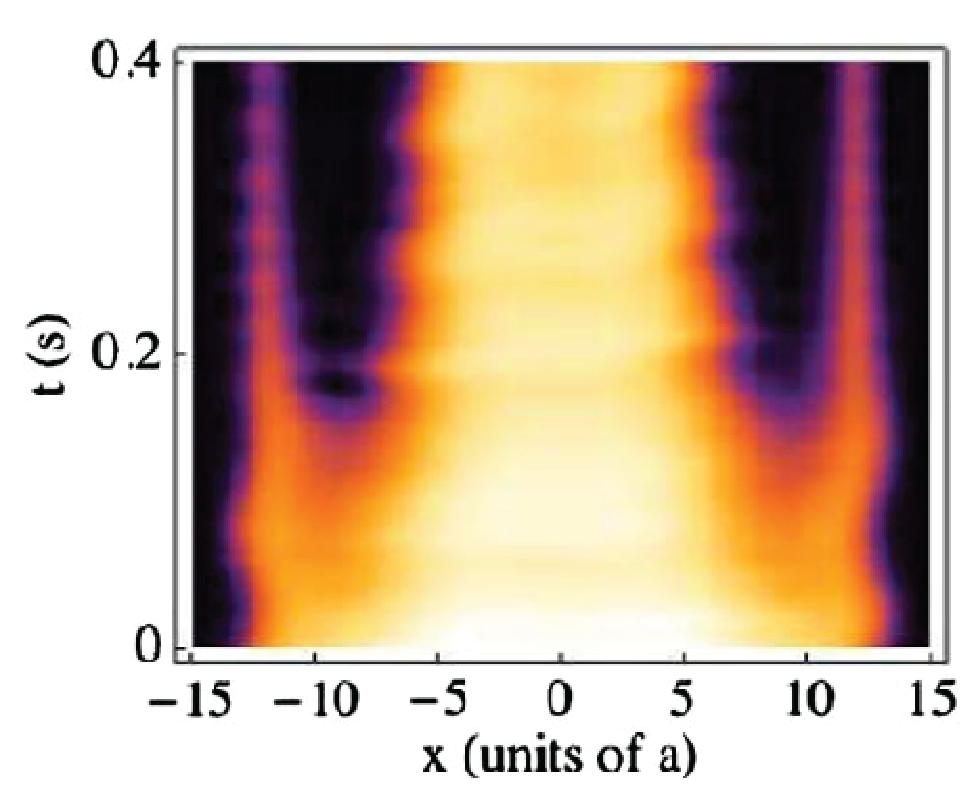
Isolated from their environment, ultracold systems are governed by quantum
coherent dynamics over very long timescales (seconds) compared to their
microscopic timescales (milliseconds). At the moment non-equilibrium
phenomena are understood on a case-by-case basis, so my choice of problems
is experimentally motivated. One problem I studied with Stefan Natu
concerned the
mechanism for equilibration in standard lattice ramps used to
create bosonic Mott insulators, with particular focus on reconciling
experimental observations. A simple but powerful time-dependent Gutwiller
mean field theory illuminated that two timescales govern the dynamics: a fast
(~ms) timescale for local relaxation and a long (~1s) timescale for transport.
This is a generic, hydrodynamic feature and has implications for creating
equilibrium states in general lattice experiments. I also am working on
explaining the anomalously slow expansion observed by Dan Stamper-Kurn's
group when tunneling is suddenly turned on in a one-dimensional lattice of
two-dimensional pancakes, with one pancake initially occupied. Using nonequilibrium Green's function
methods, we find that qualitatively this may be a form of self-trapping
(unpublished).
Quantum criticality
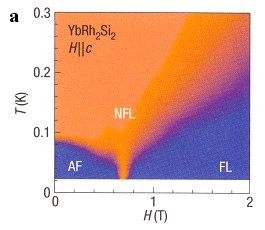
I believe that one of the most promising ways to explore "beyond quasiparticle" matter with cold atoms is
to focus on quantum critical points. A zero temperature phase diagram may display a phase transition,
in which case the quantum critical point controls the dynamics in a large "fan" of the finite temperature phase
diagram. The physics in this fan is not of the usual quasiparticle form: for example, the simple poles
in the
response functions may be replaced with various kinds of branch cuts. So far, the finite temperature
properties controlled by these points has received little
attention within the cold atoms community, perhaps due to concerns about studying criticality with relatively small numbers of particles
(10^5) and the harmonic trap, or due to the limitations in probing these systems. Because cold atoms lack the
usual transport probes,
I am presently thinking about
how quantum critical behavior observably manifests itself here. I have showed that
this physics persists in harmonic traps and one can actually exploit the
harmonic trap to
observe quantum critical phenomena.
RF spectroscopy of lattice bosons
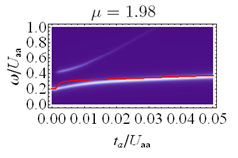
The Bose-Hubbard model's superfluid-Mott insulator phase transition is arguably the
simplest realistic and non-trivial quantum phase transition. This phase transition is realized
by ultracold bosons in an optical lattice and its properties have been explored in dimensions d=1,2,3 by
several groups,
notably by Immanuel Bloch at Mainz with
Markus Greiner (now at Harvard), at ETH Zurich by
Tilman Esslinger
at Maryland by Trey Porto
and William Phillips, and at MIT by
Wolfgang Ketterle. Because of its relatively simple theoretical
nature (compared to vexing fermionic and frustrated spin models), it is an ideal place to develop theoretical
and experimental ideas for use in future, less understood realms. One such tool we have been thinking about is
rf spectroscopy, in which an atom absorbs a low-momentum photon to change its internal state. Campbell
et al. experimentally demonstrated this to be a
useful in-situ probe of the Bose-Hubbard model's density profile.
We presented an initial sum rule analysis of
this experiment that captured the essential features and showed that the dominant
physics in these experiments is really the average two particle
correlations. Since then,
we have found that even this simple model contains surprisingly rich physics, and that the
RF spectroscopy can
directly reveal distinctly different types of correlations in the superfluid near the Mott insulator
(see also our paper).
Lattices with strong on-site correlations
I am studying the effects of increasing interaction
strengths (scattering length) in cold
atomic gases in optical lattices: more than simply increasing the Bose-Hubbard interaction scale, it
introduces extra important terms in the lattice Hamiltonian required to describe this system. The basic
idea is that if the scattering length is comparable to the interparticle spacing on a site then the wavefunction
for two or more particles on a site does not simply factor into a product of single particle wavefunctions.
For example, repulsive interactions spread out the wavefunction in a site filling-dependent way, causing a
particle-conditioned hopping rate. This alters the shape of the phase diagram.
of the phase diagram.
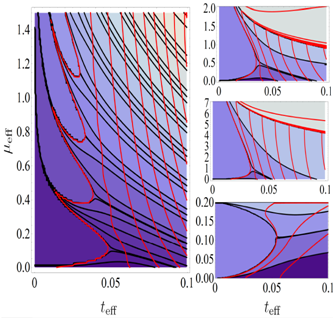
We have
argued that these effects are important for several ongoing experiments and qualitatively calculated
the model parameters:
(1) Already at the small scattering lengths in ongoing 87Rb experiments there are quantitative modifications. These
are even more important for other atomic species --- Na, Cs, Yb, etc. --- in both bosonic and fermionic
gases. One must account for this in ongoing efforts to quantitatively
emulate
condensed matter modelss, e.g. the
Fermi-Hubbard model,
with cold atomic
gases. (2) Particle-number conditioned hopping is necessary to describe rapidly
rotating sites, which earlier we proposed as a
means to
create fractional quantum Hall puddles at each lattice site. (3) Finally, attractive bosons' atomic superfluid to
molecular superfluid quantum phase transition has attracted much theoretical attention, with
proposals to use lattices to stabilize the gas; if the transition is driven via a Feshbach resonance, it is
again crucial to include our
particle conditioned hopping. We have
ongoing efforts to turn our qualitative calculations of the Hamiltonian parameters into quantitative ones using
path integral Monte Carlo methods in collaboration with John Shumway.
Quantum solids and liquids in low temperature physics
Quantum solids are solids for which the zero-point vibrations are important.
Atoms' locations are fundamentally fuzzy due to quantum fluctuations, and
additionally atoms may tunnel through several lattice sites. These systems
are often messy, involving unknown frozen-in disorder. For this price in ease
of analysis one obtains a richness
in their behavior. These systems show varieties of orbital ordering, spectral anomalies,
possible supersolidity, and glassy quantum
dynamics ---
as in solid molecular hydrogen, atomic species trapped in solid molecular hydrogen,
solid 4He , and "quantum gels," respectively. Some unpublished work can be
found in my thesis.
Cornell has
a wonderful group of low temperature experimentalists, and discussions with
Dave Lee,
John
Reppy, and their groups have been especially fun.
and their groups have been especially fun.
I also worked on a related subject that grew out of discussions with Dave Lee and Sergei Vasiliev
on quasi-2D atomic hydrogen. This is invariably adsorbed on He films, and
we
found that the He film's dynamic excitations ("ripplons")
mediate a weak, attractive interaction. In 2D, this leads to dramatic renormalizations
of the two-particle correlations. We proposed this as a consistent explanation of observed spectral anomalies.
Later investigations revealed that a simpler symmetry-based mechanism probably is behind the spectral anomalies,
but we expect the physics
of the renormalized two-particle correlations to be remain important for other reasons, for example causing a low
temperature collapse of the gas. We
also explored
anomalous spectra in solid molecular hydrogen populated with atomic hydrogen
defects.
Real materials and other past research
In reverse chronological order, I have done some work in: spin-orbit coupling in carbon nanotubes,
defects in semiconductors and metals, novel simulation algorithms (mainly accelerated Monte Carlo for computing
novel quantities such as transition rates), strongly correlated electrons, quantum computing,
and scientific feature mining and visualization... Most of these are represented in my
publication list.